 |
|
 |
|
Theory of Fuzzy Image Processing
Fuzzy image processing is a collection of different areas of fuzzy set
theory, fuzzy logic and fuzzy measure theory. The following topics represent
the most important theoretical components of fuzzy image processing:
-
Fuzzy Geometry (Metric, topology, ...)
-
Measures of Fuzziness and Image Information
(entropy, correlation, divergence, expected values, ...)
-
Fuzzy Inference Systems (image fuzzification, inference, image defuzzification)
-
Fuzzy Clustering (Fuzzy c-means, possibilistic c-means, ...)
-
Fuzzy Mathematical Morphology (Fuzzy ersion, fuzzy dilation, ...)
-
Fuzzy Measure Theory (Sugeno measure/integral,
possibility measures, necessity measures,...)
-
Fuzzy Grammars
-
Combined Approaches (Neural fuzzy/fuzzy neural approaches, fuzzy
genetic algorithms, fuzzy wavelet analysis)
-
Extension of classical methods (Fuzzy Hough transform, fuzzy median
filtering, ...)
To use the these components systematically, we need to develop a new
image understanding. The image fuzzification, therefore, plays a pivotal
role in all image processing systems that apply any of these components.
Tizhoosh distinguishes in his book between the
following kinds of image fuzzification:
-
Histogram-based gray-level fuzzification (or briefly histogram fuzzification)
Example: brightness in image enhancement (see Fig. 1)
-
Local fuzzification (Example: edge detection)
-
Feature fuzzification (Scene analysis, object recognition)
|
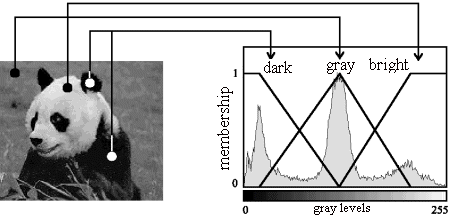
Fig.1. Histogram fuzzification (Adapted from: Tizhoosh, On a systematic
Introduction into Fuzzy Image Processing (in German). In Proc. AFN'97
Annual Meeting, Magdeburg, Germany, pp. 39-45)
|
|





